"Let's start with entropy. I'm going to mush together ideas from thermodynamics and information theory to communicate the basic underlying pattern that forms the foundation of this riddle. That means my language won't be scientifically precise, but-"
"I don't care, Nikki. I haven't taken a science exam since high school. Just give me the practical shit."
"Okay." I reached for my phone and pulled up a diagram. "Here we have a 2 x 2 grid, where half the squares are black, and half are white. If we randomly plot all the possible states we could find this system in, we notice there are 6 possible configurations of the system."

"So," I said, "what's the probability that I'll observe the system and find two black squares on the left?"
"1 in 6," Zac answered. "If there are 6 possible configurations, then the probability that you'll observe that specific configuration is 1 in 6."
"Correct. Now let's apply this to a larger 20 x 20 grid. There are gajillions of possible configurations of this system. The denominator is so large that I'll just call it n. So, what's the probability that we'll find the system in this exact state?"

"One in n," Zac replied.
"Very good. What about this one?"

"One in n," Zac answered again.
"Perfect. Both of these configurations have the same probability of being observed. Now let's zoom out and observe the system as a generalized whole. For simplicity's sake, let's say all black squares represent particles. If you look closely, you'll notice that the 'random' configuration has an even distribution of particles, whereas the 'half-half' configuration has an uneven distribution of particles."
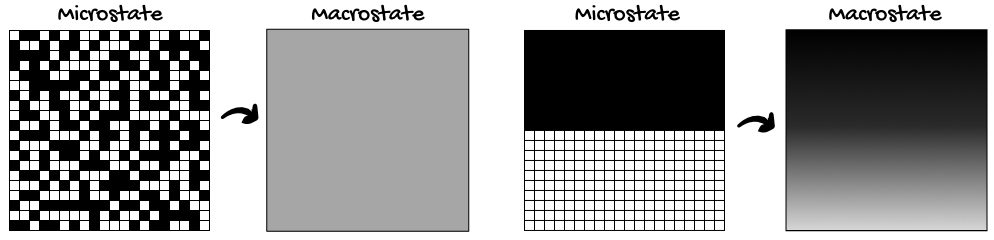
"There are many, many possible configurations that give the system an even distribution of particles. To get an uneven distribution, the particles can only be arranged in a limited number of ways. Which brings me to my next point. Imagine you saw these two snapshots of a system…"

"Which snapshot came first: the evenly-spread-out one, or the half-half one?" I asked.
"Umm… the half-half one," Zac answered.
"Why?"
Zac pulled an ice cube from the container in his lap and held it in his hand. "Because things naturally move from ordered to disordered states over time."
We watched the ice cube slowly begin to melt onto Zac's warm palm.
"Now," I said, "it's not that the ice cube is necessarily moving into a 'disordered' state. The ice cube is just moving to the highest probability state available, given the laws of physics. The particles in an ice cube can only be arranged in a limited number of ways, in order to remain an ice cube. The particles in a liquid have more freedom. Therefore, when an ice cube melts, it goes from a low probability state to a high probability state, until it reaches a smoothly spread-out equilibrium."
"Is low probability the same as 'low entropy?'" Zac asked.
"You could say that," I said. "As the system moves from low probability to high probability states, we say the entropy increases."
"Okay," Zac mused. "So if I put this ice cube in a box, that system has low entropy because all the particles are bunched up in one corner? But once it melts and the liquid spreads out evenly, it has higher entropy?"
"Yes," I said. "As another example, the 'half-half' configuration has low entropy because the particles are in a restricted, low-probability state. The evenly-spread-out configuration has high entropy because there are many more particle configurations that give this smooth, even distribution of particles."
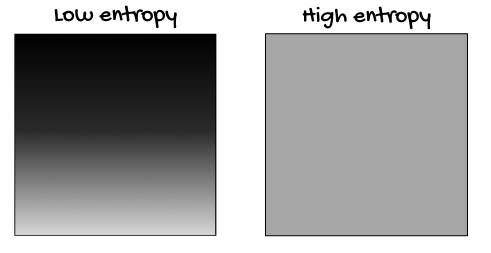
"Can you see how the energy spreads out to a smooth, even equilibrium over time?" I asked.
"Yeah," Zac replied.
"Good. It's important to understand that everything in the universe is doing this. This is the second law of thermodynamics: the entropy of an isolated system always stays the same or increases over time."
"What's the first law of thermodynamics?" Zac asked.
"Energy cannot be created or destroyed in an isolated system — it can only change form. We've already talked about that, remember? I explained why we'd expect that law if the universe is a giant neural network."
Zac nodded.
"Well, we'd also expect the second law of thermodynamics if the universe is a giant neural network that is self-organizing according to this mysterious algorithm I've mentioned. This algorithm predicts that entropy would increase over time."
"How come?"
"I need to lay down a few foundations to get there, so-"

